勾股定理是世界上最伟大的定理之一,是用代数思想解决几何问题的重要工具,也是数形结合的纽带,周老师在上八年级《从勾股定理到图形面积关系的拓展》一节拓展课时,教学环节清晰,内容安排有序,问题设计合理(如下),作为课堂主人的你,请积极思考解决下列问题:【知识回顾】勾股定理反映了直角三角形三条边之间的关系:a2+b2=c2,而a2,b2,c2又可以看成是以a,b,c为边长的正方形面积,因此,勾股定理也可以表述为:分别以直角三角形两条直角边为边长的两个正方形的面积之和,等于以斜边为边长的正方形的面积(如图1),即S
2019-05-07
勾股定理是世界上最伟大的定理之一,是用代数思想解决几何问题的重要工具,也是数形结合的纽带,周老师在上八年级《从勾股定理到图形面积关系的拓展》一节拓展课时,教学环节清晰,内容安排有序,问题设计合理(如下),作为课堂主人的你,请积极思考解决下列问题:
【知识回顾】
勾股定理反映了直角三角形三条边之间的关系:a2+b2=c2,而a2,b2,c2又可以看成是以a,b,c为边长的正方形面积,因此,勾股定理也可以表述为:分别以直角三角形两条直角边为边长的两个正方形的面积之和,等于以斜边为边长的正方形的面积(如图1),即S1+S2=S3.
【问题探究】

(1)如果以直角三角形三条边a,b,c为直径,向形外分别作半圆(如图2),那么三个半圆的面积为S1,S2,S3之间存在怎样的关系?请直接写出你认为正确的结论:___;
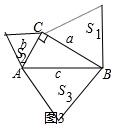
(2)类似地,上述结果是否适合其他图形?适合的,请你在图3中以直角三角形的三条边a,b,c为边,向形外画出图形(示意图),指出你所画的图形名称是:___,并写出证明过程;不存在的,请说明理由.
【拓展应用】
(1)如图4,已知在Rt△ABC中,∠ACB=Rt∠,AB=4,分别以AC、BC为直径作半圆,面积分别记为S2、S1,则S1+S2的值等于___;
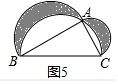
(2)在Rt△ABC中,∠BAC=Rt∠,分别以AB,AC为直径作半圆,以BC为直径作半圆刚好经过点A(如图5所示),若AB=4,AC=3,则两个月牙形(阴影部分)的面积之和即S1+S2=___.
【知识回顾】
勾股定理反映了直角三角形三条边之间的关系:a2+b2=c2,而a2,b2,c2又可以看成是以a,b,c为边长的正方形面积,因此,勾股定理也可以表述为:分别以直角三角形两条直角边为边长的两个正方形的面积之和,等于以斜边为边长的正方形的面积(如图1),即S1+S2=S3.
【问题探究】

(1)如果以直角三角形三条边a,b,c为直径,向形外分别作半圆(如图2),那么三个半圆的面积为S1,S2,S3之间存在怎样的关系?请直接写出你认为正确的结论:___;
(2)类似地,上述结果是否适合其他图形?适合的,请你在图3中以直角三角形的三条边a,b,c为边,向形外画出图形(示意图),指出你所画的图形名称是:___,并写出证明过程;不存在的,请说明理由.
【拓展应用】
(1)如图4,已知在Rt△ABC中,∠ACB=Rt∠,AB=4,分别以AC、BC为直径作半圆,面积分别记为S2、S1,则S1+S2的值等于___;
(2)在Rt△ABC中,∠BAC=Rt∠,分别以AB,AC为直径作半圆,以BC为直径作半圆刚好经过点A(如图5所示),若AB=4,AC=3,则两个月牙形(阴影部分)的面积之和即S1+S2=___.