优质解答
令f(x)>0,得:kx+4>
,
令g(x)=
,则g′(x)=
,
令g′(x)>0,解得:x>e,令g′(x)<0,解得:1<x<e,
故g(x)在(1,e)递增,在(e,+∞)递减,
画出函数草图,如图示:
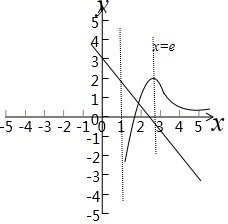 ,
,
结合图象
,解得:
-2<k≤
-
,
故答案为:(
-2,
-
].
令f(x)>0,得:kx+4>
,
令g(x)=
,则g′(x)=
,
令g′(x)>0,解得:x>e,令g′(x)<0,解得:1<x<e,
故g(x)在(1,e)递增,在(e,+∞)递减,
画出函数草图,如图示:
 ,
,
结合图象
,解得:
-2<k≤
-
,
故答案为:(
-2,
-
].
| x |
| lnx |
令g(x)=
| x |
| lnx |
| lnx-1 |
| (lnx)2 |
令g′(x)>0,解得:x>e,令g′(x)<0,解得:1<x<e,
故g(x)在(1,e)递增,在(e,+∞)递减,
画出函数草图,如图示:
 ,
,结合图象
|
| 1 |
| ln2 |
| 1 |
| ln3 |
| 4 |
| 3 |
故答案为:(
| 1 |
| ln2 |
| 1 |
| ln3 |
| 4 |
| 3 |
| x |
| lnx |
令g(x)=
| x |
| lnx |
| lnx-1 |
| (lnx)2 |
令g′(x)>0,解得:x>e,令g′(x)<0,解得:1<x<e,
故g(x)在(1,e)递增,在(e,+∞)递减,
画出函数草图,如图示:
 ,
,结合图象
|
| 1 |
| ln2 |
| 1 |
| ln3 |
| 4 |
| 3 |
故答案为:(
| 1 |
| ln2 |
| 1 |
| ln3 |
| 4 |
| 3 |