如图,一条抛物线y=14x2+m(m<0)与x轴相交于A、B两点(点A在点B的左侧).若点M、N的坐标分别为(0,-2)、(4,0),抛物线与直线MN始终有交点,线段AB的长度的最小值为2727.
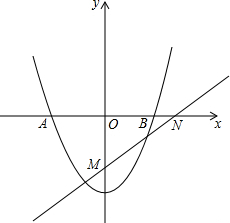 如图,一条抛物线y=
如图,一条抛物线y=
x2+m(m<0)与x轴相交于A、B两点(点A在点B的左侧).若点M、N的坐标分别为(0,-2)、(4,0),抛物线与直线MN始终有交点,线段AB的长度的最小值为
2019-05-03
 如图,一条抛物线y=
如图,一条抛物线y=| 1 |
| 4 |
2
| 7 |
2
.
| 7 |