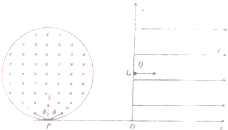
(2013•淄博三模)如图所示,在直角坐标系xOy的第一象限内,有场强大小为E,方向沿x轴正方向匀强磁场,第二象限内有一半径为l0的圆形匀强磁场区域,磁场方向垂直于xOy平面向里,圆形磁场边缘与x轴相切与P点,P点坐标为(-2l0,0)现有三个电子a,b,c从P点以相同速率沿不同方向同时射入匀强磁场区域,其中电子b射入方向沿y轴正方向,电子a,c与电子b速度方向夹角均为θ=π3.电子经过磁场偏转后恰都垂直于y轴方向进去第一象限,电子b经过y轴上的Q(0,l0)点进去第一象限,电子a,c进去第一象限前在磁场
 (2013•淄博三模)如图所示,在直角坐标系xOy的第一象限内,有场强大小为E,方向沿x轴正方向匀强磁场,第二象限内有一半径为l0的圆形匀强磁场区域,磁场方向垂直于xOy平面向里,圆形磁场边缘与x轴相切与P点,P点坐标为(-2l0,0)现有三个电子a,b,c从P点以相同速率沿不同方向同时射入匀强磁场区域,其中电子b射入方向沿y轴正方向,电子a,c与电子b速度方向夹角均为θ=
(2013•淄博三模)如图所示,在直角坐标系xOy的第一象限内,有场强大小为E,方向沿x轴正方向匀强磁场,第二象限内有一半径为l0的圆形匀强磁场区域,磁场方向垂直于xOy平面向里,圆形磁场边缘与x轴相切与P点,P点坐标为(-2l0,0)现有三个电子a,b,c从P点以相同速率沿不同方向同时射入匀强磁场区域,其中电子b射入方向沿y轴正方向,电子a,c与电子b速度方向夹角均为θ=
.电子经过磁场偏转后恰都垂直于y轴方向进去第一象限,电子b经过y轴上的Q(0,l0)点进去第一象限,电子a,c进去第一象限前在磁场中运动的时间差是t0.已知三个电子恰都经过同一点K(图中未画出),电子质量m、电荷量为e,不计重力,求:
(1)匀强磁场的磁感应强度大小B;
(2)电子在电场中运动离y轴的最远距离d;
(3)K点的坐标及三个电子到达K点的时间差.
2019-04-29
 (2013•淄博三模)如图所示,在直角坐标系xOy的第一象限内,有场强大小为E,方向沿x轴正方向匀强磁场,第二象限内有一半径为l0的圆形匀强磁场区域,磁场方向垂直于xOy平面向里,圆形磁场边缘与x轴相切与P点,P点坐标为(-2l0,0)现有三个电子a,b,c从P点以相同速率沿不同方向同时射入匀强磁场区域,其中电子b射入方向沿y轴正方向,电子a,c与电子b速度方向夹角均为θ=
(2013•淄博三模)如图所示,在直角坐标系xOy的第一象限内,有场强大小为E,方向沿x轴正方向匀强磁场,第二象限内有一半径为l0的圆形匀强磁场区域,磁场方向垂直于xOy平面向里,圆形磁场边缘与x轴相切与P点,P点坐标为(-2l0,0)现有三个电子a,b,c从P点以相同速率沿不同方向同时射入匀强磁场区域,其中电子b射入方向沿y轴正方向,电子a,c与电子b速度方向夹角均为θ=| π |
| 3 |
(1)匀强磁场的磁感应强度大小B;
(2)电子在电场中运动离y轴的最远距离d;
(3)K点的坐标及三个电子到达K点的时间差.
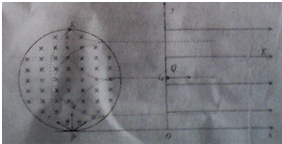 (1)设电子在匀强磁场中运动的周期为T,电子a、c在磁场中分别转过30°和150°圆心角,则运动时间分别为:
(1)设电子在匀强磁场中运动的周期为T,电子a、c在磁场中分别转过30°和150°圆心角,则运动时间分别为: