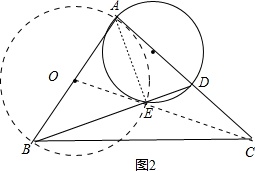
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4 2 ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为.
2019-05-03
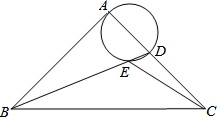
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为___.
| | 2 |

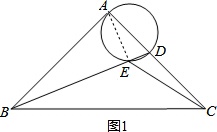 连结AE,如图1,
连结AE,如图1,